Bridge Crane designs and ideas...38' span

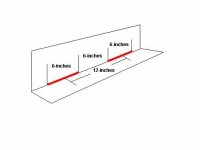
[LD1]

Ld
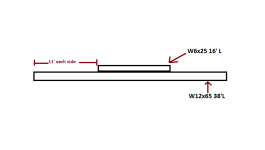
Is there an 18 deep beam in your table with similar flange to the small beam. If yes the two beams welded together would be a slightly stronger beam

I wish. The 6x12 has a 4" flange that is 0.280" thick. The lightest 18" beam 6" x 0.425" flange. And that light 18" beam has a smaller moment than teh w12x65 I would be starting with. So that dont work out.

There was this program called "beam boy" that would calculate all sorts of data related to beams and deflection and loading. I can't remember if you could give it custom shapes. You might try looking into that.

For Android smartphones there is an app called epic FEM, but doesn't allow custom shapes far as I know.

Beam boy dont allow custom shapes. (I use beam boy alot). Also tried a couple more beam tools I downloaded, but dont allow custom shapes.

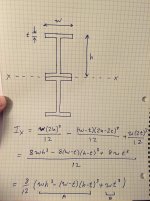
I'm even drawing a blank on the moment calculations by breaking down into individual shapes.

 

[Shield Arc]

Ld
How would the two beam attach to each other? Bolted , continuous weld, intermittent weld
This would affect the strength

I would skip weld it. Most likely go with 6 on 12 weld, and back step it.

 

[CNC Dan]

I'm even drawing a blank on the moment calculations by breaking down into individual shapes.

I'll take a look in my book tonight an see if I can find it.

 

[s219]

Well, if you guys want to make life easier on yourselves, it's just integration -- simple calculus. I don't bother remembering beam formulas (other than simple ones) knowing I can quickly derive them on the fly. My head doesn't have room for all the recipes in the cookbook, so I just remember how to cook from scratch.

Another way you can do complex shapes is to do a full area and then delete the air. So for example, you can compute for an i-beam by doing the full rectangle and then delete the air on each side of the web. For two stacked i-beams, do the full rectangle and then delete the 4 sections of air.

Take advantage of symmetry and just do half the beam (split vertically) and then double the answer.

Parallel axis theorem (google it) can be used to shift moment of inertia from one axis to another. So you can compute about the central axis of the simple shape parts and then transfer to the central axis of the complex shape to add in to the total.

For tallish i-beams where the flange spacing is much greater than the flange width, I bet two stacked beams (assumed to be joined perfectly) will only be fractionally better than a single i-beam of the same total height and web/flange thicknesses. Reason being is that the two joined flanges in the middle are too close to the central axis to have much of an area moment of inertia about that axis. The best way to get area moment of inertia is to have the area far from the central axis. Stuff close in doesn't contribute as much.

 

[s219]

OK, here's an equation that will work for stacked w-beams of uniform web/flange thickness. Can be modified to an i-beam with a little work, or to accommodate different web/flange thickness.

To get this I did the full rectangle, minus the air if the middle flanges were ignored, and then added back in the middle flanges. That allows all moment calculations to refer to a single central axis and lets us do a comparison at the end.

In the final answer, terms "A" would be for a full w-beam of the same total height. The "B" term is the added area moment from the two flanges in the middle, so it gives the contribution of stacking the beams.

 

[s219]

So as an example, with h=10", w=3", and t=0.25", the stacked beams give Ix=300.8 in^4. A single beam of the same total height as the stack (so same but no flanges in the middle) has Ix=300.7 in^4. Essentially no real difference.

Based on this, I think that for tallish i-beams or w-beams where the height is 3X the width or better, you may as well just assume that two stacked/joined beams are more or less the same in bending as a single beam of the same height as the stack. That ought to really simplify your calculations.

Again, this assumes the stacked beams are joined perfectly, or in such a way that the joint isn't an issue. You should be able to calculate what type of bolting or welding is required to meet that assumption. Along the central axis of the beam, all the loads are shear loads; there is no tension/compression.

 

[LD1]

Parallel axis theorem.....just the missing piece I was looking for.

Found this....nice video https://www.youtube.com/watch?v=WDdkdC1sFQQ

Working out the numbers for the following....

W12x65 beam
Wf = 12.000
Tf = .605
Tw = .390
Height = 12.1

I come up with Ix = 519 Pretty close. Beam is actually listed at 533 due to the radius I didnt account for. But proved to myself the formula works.

Adding a W6x12 beam underneath...
Wf = 4.00"
Tf = 0.280"
Tw = 0.230"
Height = 6.03"
Ix all by itself... 22.1

Stacking them I get Ix = 759. And in reality probably closer to 800 since I didnt account for the radius where web meets flange.

Dont really gain anything in the way of lifting capacity though.:thumbdown: If I use Bending stress as the ultimate limiting factor. Keeping it 5:1 for safety limits max stress to 7200psi. Adding height to the beam dont do any favors in that department since the beam height (or rather 1/2 the beam height c) is part of that equation.

But what it does do is decrease deflection by about 50%.

Results...single W12x65 beam, 38' span, 5k load in the middle....~6650psi stress, 0.634" deflection
Stacked beams same load and span.........................................~6800psi stress, 0.434" deflection

 

[farmer2009]

How much strength could you add to those beams by adding a top truss?

 

[LD1]

How much strength could you add to those beams by adding a top truss?

I would guess not much. Since the top is in compression and not tension. IF it was a cantilever design, (kinda like a cherry picker) where the top is in tension, then it would be significant. And adding more "light" material making the beam taller seems to have an adverse effect on the stress. While it makes a stiffer beam, it dont really help in the stress department.

I like all this learning and learning new formulas and how to apply them. (thanks S219)

Now on to my next question....and this may be getting into the realm of needing software but I dont know....

The weakest part of the beam is right in the middle. Looking at alot of multi-ton industrial cranes, (and even steel buildings) the "members" get smaller toward the edges. Cause the strength is needed in the middle.

So consider this design and see if anyone has any way to calculate it out.....

Alot of the beams are going to require cutting/splicing (used market for ya).

So what about say.....A w12x65 beam 38' long, but another beam ON TOP, but perhaps not full lenght. I have an assortment of beams on the rack now that could be welded to the top centered up (and likely bridging over whatever splice I need to make)

I have some W8x28 maybe 15' long, Some S10x25.4 about 12' long, some W4x13 about 15' long, as well as some 4x6 and 6x6 1/4 wall box tube, and a C12x20.7 channel about 10' long.

I could use any of these to cap the beam in the middle centered up....but how to calculate that?

 

[Streetcar]

Ld1
Differing sections can be used. You just calculate the beam loads and strengths in the various composite sections you have made.
In most cases welding is easier to join beams verses bolting.
Your calculation for moment of inertia is lower than beam value, Because the beam flanges are slightly tapered. They are thicker near the web
Additional information. Roadways use bolted connection in many cases because of repetitive loads from vehicle, millions of trucks can cause problems with welded connections. Shop crane will not have this issue.

Good luck

 

[LD1]

Your calculation for moment of inertia is lower than beam value, Because the beam flanges are slightly tapered. They are thicker near the web

These are W-type beams, not S-type, so the flanges are uniform thickness. Whats not accounted for is the radius where the web meets the flange.

I could find the radius and calculate that, but given the small amount I didnt feel it was worth the time to calculate. So just calculating it as square and using a 5:1SF....I might have a 5.1:1 SF when all said and done.

IOW, I am not concerned about the extra 10# I might be able to lift figuring in the radius.

 

[Streetcar]

Rolling the beam in the mill induces a taper. S type is more severe than W, but both have the taper

 

[LD1]

Rolling the beam in the mill induces a taper. S type is more severe than W, but both have the taper

I dont buy this.

I have 3 w-type beams on my rack.

W4x13
W6x12
W6x25 (I mis-spoke earlier. I was thinking this was a W8 but it isnt).

Of these 3 beams, measuring the flanges at the edge and near the web with micrometers, there isnt more than .003" in any of my measurements. Likely surface rust and mill scale variations.

What there is though, on the W4x13 beam is a 0.250" radius, W6x12 = 0.375" radius and the W6x25 is a 0.500" radius according to my gauges. The radius I believe is the ONLY thing that accounts for factoring a slightly lower Ix4 than published spec.

But its a moot point. IF anyone knows how to calculate stacked beams where they are only stacked in the center part of the beam for a given length I am all ears.

IE: like this...

 

[Streetcar]

Ld
For the portion of the beam of the beam that is stacked. You would calculate loading based on that section. For the portion of single beam you would calculate based on the single beam strength.

If you have noticed bridges with reduced weight limits, this is how the reduced limit is calculated based on deterioration of the steel beams. Different beam section give different loadings

 

[LD1]

Ld
For the portion of the beam of the beam that is stacked. You would calculate loading based on that section. For the portion of single beam you would calculate based on the single beam strength.

Example? Formulas?

All of the load assuming load at midspan, is going to be on the double stacked part.

Simple enough to calculate a double stack (now that I know how) prvided it is double stacked the entire length.

But what if the stacked section were 6' shorter? or 12' shorter? or 22' shorter like my examle? How does that effect total capacity.

Lots of MFG bridge cranes taper down at the ends. The extra mass is not needed there as on long spans, beam shear near the supports is rarely an issue, rather stress and deflection near the mid-point. But where the beam is narrower at the ends....how far can that be cheated out and still maintain full strength? and beyond that....how much increase or reduction in capacity at varying lengths of the second beam?

 

[Streetcar]

For the 11 ft at each end calculate as single beam . For the middle calculate as double beam. You make load chart by combining the appropriate section of the charts from each beam section

You can make as many steps in the beam as you like. I have worked on old bridges with up to four different beam sections. For rating bridges, the beam was rated at the tenth points of each span typically.

Shear in beam is controlled by area of the area not its shape

What are you using to calculate stress and deflection. I ca explain easier after I look at the results?

 

[Streetcar]

Ld
For the end 11 ft the beam will have the stress and deflections as if a single beam was loaded for the entire span. The middle will act as double beam for stress , but will have higher deflection. The deflection will be less than single beam though. I hope this helps explain load ratings.

Dave

 

[LD1]

I made a spread sheet with all the W-types and all the S-type beams listed ranging from W10x12 up to W24x104. (I didnt list the super heavy 100+ PLF beams like a W14x600).

After I made the list, the only two beam specs needed was the c (distance from neutral axis to farthest fiber) and the i4.

After that I used the formulas for stress and deflection

Stress = cWl/4i
Deflection Wl^3/48Ei

Gave each beam a max capacity based on stress failure at 36ksi, and its deflection right beside that

Then gave a WLL assuming 5:1 SF so limiting stress to 7200psi, and listed its deflection beside that.

I also use Beamboy. But got tired of trying to remember all the beams and what they can handle. So I made the spread sheet. Gives the same basic info.

Also used a trial version of StruCalc 9.0. They have a pretty nice feature where you can input the beam, span, load, bracing, etc. Then choose a W12 beam and it will list the minimum requirements. So I did that with loads from 2k to 10k going up 1k at a time, and beams from 10" to 24" and made a chart. IE: Y axis shows loads from 2k, 3k, 4k,etc. X-axis is 10", 12", 14", etc beams.

That program matches up pretty well with the other ways I was calculating.

I am still lost on how to calculate the double beams. IF you have the time, could you walk me through an example. Even if its simplified. Like a 20' span and 10' beam in the middle to make things easy.

 

[s219]

Couple tricks can be used for what is basically a beam of variable cross-section.

One way (and this works in both directions) is to replace that double section of beam with something that has the same cross section (I) but assumes a much stronger material. You can use the ratio of I to determine the ratio of E, since they are side beside in most beam equations (i.e., if I is double, then replace with double E instead). However, you would still need to take into account the weakest E at some point, to make sure the actual stresses don't exceed it. This method is often used in reverse for composite beams, say an I-beam with wood lumber sistered in -- I'd replace the lumber with a smaller chunk of steel that has the same net E*I, but later check back to see that the resulting stresses are acceptable for the weaker material -- wood.

The other way is to break the calculation into sections, and label all the unknowns. Draw imaginary saw lines through the point where the single and stacked beam sections meet, and then replace the "connection" with lateral and vertical forces and a twisting moment -- basically, the forces and moments that were otherwise holding the beam together before you sawed it apart. The deflection at the end of the section of single beam will be the starting deflection for the section of double beam. You should be able to solve for all the forces and moments by doing sums in the horizontal and vertical directions, and sums of moments, for each of the sections you sawed apart.

I'll try to draw a sketch if I get a minute today, but hopefully the description makes sense.

 

[s219]

OK, here are a couple derivations that should help. First, for background, here is how a simple beam formula is derived using the differential equation for the elastic curve of a beam, which relates moment to curvature and material/shape properties:



That gives the well known deflection for a beam with simple supports and a point load in the middle.

Here's the same approach but for a beam that has a different area moment in the middle section. For convenience I assumed the beam is evenly spaced up in quarters, with the different section taking up the middle half.



I checked to make sure this more complex formula gave the simple result when the area moment was the same everywhere, and it does, which hopefully is a good check on my math. But it couldn't hurt to follow through and check my work. Really the hardest part of these derivations is not the Calculus, it's keeping track of all the math and fractions.

The basic gist of what I did in the second case was the same derivation, but breaking it down to apply to different sections of the beam. We can solve for unknown constants in the process by knowing deflection is zero at the end, that slope is zero in the middle at x=L/2, and that deflection and slope must be equal where the two different sections meet up at x=L/4. That lets us come up with equations for the whole beam.

Anyhow, using the result on page 4, you can plug in I1 (unstacked area moment) and I2 (stacked area moment) and get the deflection in the middle of the beam. Hope this helps!